Логарифм это свойства и противопоказания
Многие школьники считают логарифмы сложной темой в курсе математики. Но если разобрать, что такое логарифм подробно, от простого к сложному, то на ЕГЭ вы не станете их опасаться.
Часто у учеников возникает путаница, где аргумент, а где основание логарифма. И что же нужно возвести в степень, чтобы этот логарифм, наконец, посчитать.
В этой статье мы откроем секрет, как легче запомнить принцип решения логарифма.
Итак, давайте разбираться, что такое логарифм.
- Что такое логарифм и как его посчитать
- Зачем логарифмам специальные обозначения
- Основные свойства логарифмов — все формулы в одном месте
- 10 примеров логарифмов с решением
Что такое логарифм и как его посчитать
Логарифм имеет следующий вид:
где a – это основание логарифма,
b – это аргумент логарифма
Чтобы узнать значение логарифма приравняем его к X.
и преобразовываем в
Запомните, что именно основание (оно выделено красным) возводится в степень.
Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!
Приведем пример:
Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:
А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом:
Еще раз обращаю ваше внимание, что основание (в нашем случае это – 2) всегда находится внизу и именно оно возводится в степень.
Еще примеры:
Логарифмы со специальным обозначением
Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.
Десятичный логарифм
Десятичный логарифм обозначается lg и имеет основание 10, т.е.
Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.
Например, вычислим lg100
Натуральный логарифм
Натуральный логарифм обозначается ln и имеет основание e, то есть
Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…
Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что
И вычислить его можно таким образом:
Основные свойства логарифмов
Логарифмы можно преобразовывать, но для этого необходимо знать правила, которые называются основными свойствами логарифмов. Данные свойства обязательно нужно знать каждому ученику! Без знания этих свойств невозможно решить ни одну серьезную логарифмическую задачу. Вот эти свойства:
Совет – тренируйтесь применять эти свойства в обе стороны, то есть как слева направо, так и справа налево!
Рассмотрим свойства логарифмов на примерах.
Логарифмический ноль и логарифмическая единица
Это следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор.
Запомните, что логарифм от a по основанию а всегда равен единице:
loga a = 1 – это логарифмическая единица.
Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a0 = 1:
loga 1 = 0 – логарифмический ноль.
Основное логарифмическое тождество
В первой формуле число m становится степенью, которая стоит в аргументе. Данное число может быть любым. Некоторые выражения могут быть решены только с помощью этого тождества.
Вторая формула по сути является просто переформулированным определением логарифма
Разберем применение тождества на примере:
Необходимо найти значение выражения
Сначала преобразуем логарифм
Вернемся к исходному выражению и применим правило умножения степеней с одинаковым основанием:
Теперь применим основное логарифмическое тождество и получим:
Сумма логарифмов. Разница логарифмов
Логарифмы с одинаковыми основаниями можно складывать:
Логарифмы с одинаковыми основаниями можно вычитать:
Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!
Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!
Вынесение показателя степени из логарифма
Вынесение показателя степени из логарифма:
Переход к новому основанию
Когда мы разбирали формулы суммы и разности логарифмов, то обращали внимание на то, что основания логарифмов должны быть при этом одинаковыми. А что же делать, если основания логарифмов разные? Воспользоваться свойством перехода к новому основанию.
Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.
Разберем на примере.
Необходимо найти значение такого выражения
Для начала преобразуем каждый логарифм с помощью свойства вынесения показателя степени из логарифма:
Теперь применим переход к новому основанию для второго логарифма:
Подставим полученные результаты в исходное выражение:
10 примеров логарифмов с решением
1. Найти значение выражения
2. Найти значение выражения
3. Найти значение выражения
4. Найти значение выражения
5. Найти значение выражения
6. Найти значение выражения
Сначала найдем значение
Для этого приравняем его к Х:
Тогда изначальное выражение принимает вид:
7. Найти значение выражения
Преобразуем наше выражение:
Теперь воспользуемся свойством вынесения показателя степени из логарифма и получим: 
8. Найти значение выражения
Так как основания логарифмов одинаковые, воспользуемся свойством разности логарифмов:
9. Найти значение выражения
Так как основания логарифмов разные, применять свойство суммы логарифмов нельзя. Поэтому решаем каждый логарифм по отдельности:
Подставляем полученные значения в исходное выражение:
4 + 3 = 7
10. Найти значение выражения
Обращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log216. Поэтому сначала найдем значение log216, а затем подставим полученный результат в log4:
Надеюсь, теперь вы разобрались, что такое логарифм.
Источник
2 февраля 2017
- Скачать все формулы
Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы — это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами.
Эти правила обязательно надо знать — без них не решается ни одна серьезная логарифмическая задача. К тому же, их совсем немного — все можно выучить за один день. Итак, приступим.
Сложение и вычитание логарифмов
Рассмотрим два логарифма с одинаковыми основаниями: logax и logay. Тогда их можно складывать и вычитать, причем:
- logax + logay = loga (x · y);
- logax − logay = loga (x : y).
Итак, сумма логарифмов равна логарифму произведения, а разность — логарифму частного. Обратите внимание: ключевой момент здесь — одинаковые основания. Если основания разные, эти правила не работают!
Эти формулы помогут вычислить логарифмическое выражение даже тогда, когда отдельные его части не считаются (см. урок «Что такое логарифм»). Взгляните на примеры — и убедитесь:
Задача. Найдите значение выражения: log6 4 + log6 9.
Поскольку основания у логарифмов одинаковые, используем формулу суммы:
log6 4 + log6 9 = log6 (4 · 9) = log6 36 = 2.
Задача. Найдите значение выражения: log2 48 − log2 3.
Основания одинаковые, используем формулу разности:
log2 48 − log2 3 = log2 (48 : 3) = log2 16 = 4.
Задача. Найдите значение выражения: log3 135 − log3 5.
Снова основания одинаковые, поэтому имеем:
log3 135 − log3 5 = log3 (135 : 5) = log3 27 = 3.
Как видите, исходные выражения составлены из «плохих» логарифмов, которые отдельно не считаются. Но после преобразований получаются вполне нормальные числа. На этом факте построены многие контрольные работы. Да что контрольные — подобные выражения на полном серьезе (иногда — практически без изменений) предлагаются на ЕГЭ.
Вынесение показателя степени из логарифма
Теперь немного усложним задачу. Что, если в основании или аргументе логарифма стоит степень? Тогда показатель этой степени можно вынести за знак логарифма по следующим правилам:
- logaxn = n · logax;
-
-
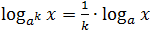
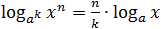
Несложно заметить, что последнее правило следует их первых двух. Но лучше его все-таки помнить — в некоторых случаях это значительно сократит объем вычислений.
Разумеется, все эти правила имеют смысл при соблюдении ОДЗ логарифма: a > 0, a ≠ 1, x > 0. И еще: учитесь применять все формулы не только слева направо, но и наоборот, т.е. можно вносить числа, стоящие перед знаком логарифма, в сам логарифм. Именно это чаще всего и требуется.
Задача. Найдите значение выражения: log7 496.
Избавимся от степени в аргументе по первой формуле:
log7 496 = 6 · log7 49 = 6 · 2 = 12
Задача. Найдите значение выражения:
[Подпись к рисунку]
Заметим, что в знаменателе стоит логарифм, основание и аргумент которого являются точными степенями: 16 = 24; 49 = 72. Имеем:
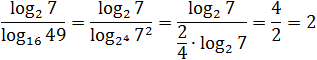[Подпись к рисунку]
Думаю, к последнему примеру требуются пояснения. Куда исчезли логарифмы? До самого последнего момента мы работаем только со знаменателем. Представили основание и аргумент стоящего там логарифма в виде степеней и вынесли показатели — получили «трехэтажную» дробь.
Теперь посмотрим на основную дробь. В числителе и знаменателе стоит одно и то же число: log2 7. Поскольку log2 7 ≠ 0, можем сократить дробь — в знаменателе останется 2/4. По правилам арифметики, четверку можно перенести в числитель, что и было сделано. В результате получился ответ: 2.
Переход к новому основанию
Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. А что, если основания разные? Что, если они не являются точными степенями одного и того же числа?
На помощь приходят формулы перехода к новому основанию. Сформулируем их в виде теоремы:
Пусть дан логарифм logax. Тогда для любого числа c такого, что c > 0 и c ≠ 1, верно равенство:
[Подпись к рисунку]
В частности, если положить c = x, получим:
[Подпись к рисунку]
Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.
Эти формулы редко встречается в обычных числовых выражениях. Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств.
Впрочем, существуют задачи, которые вообще не решаются иначе как переходом к новому основанию. Рассмотрим парочку таких:
Задача. Найдите значение выражения: log5 16 · log2 25.
Заметим, что в аргументах обоих логарифмов стоят точные степени. Вынесем показатели: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;
А теперь «перевернем» второй логарифм:
[Подпись к рисунку]
Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами.
Задача. Найдите значение выражения: log9 100 · lg 3.
Основание и аргумент первого логарифма — точные степени. Запишем это и избавимся от показателей:
[Подпись к рисунку]
Теперь избавимся от десятичного логарифма, перейдя к новому основанию:
[Подпись к рисунку]
Основное логарифмическое тождество
Часто в процессе решения требуется представить число как логарифм по заданному основанию. В этом случае нам помогут формулы:
- n = logaan
-
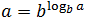
В первом случае число n становится показателем степени, стоящей в аргументе. Число n может быть абсолютно любым, ведь это просто значение логарифма.
Вторая формула — это фактически перефразированное определение. Она так и называется: основное логарифмическое тождество.
В самом деле, что будет, если число b возвести в такую степень, что число b в этой степени дает число a? Правильно: получится это самое число a. Внимательно прочитайте этот абзац еще раз — многие на нем «зависают».
Подобно формулам перехода к новому основанию, основное логарифмическое тождество иногда бывает единственно возможным решением.
Задача. Найдите значение выражения:
[Подпись к рисунку]
Заметим, что log25 64 = log5 8 — просто вынесли квадрат из основания и аргумента логарифма. Учитывая правила умножения степеней с одинаковым основанием, получаем:
[Подпись к рисунку]
Если кто-то не в курсе, это была настоящая задача из ЕГЭ 🙂
Логарифмическая единица и логарифмический ноль
В заключение приведу два тождества, которые сложно назвать свойствами — скорее, это следствия из определения логарифма. Они постоянно встречаются в задачах и, что удивительно, создают проблемы даже для «продвинутых» учеников.
- logaa = 1 — это логарифмическая единица. Запомните раз и навсегда: логарифм по любому основанию a от самого этого основания равен единице.
- loga 1 = 0 — это логарифмический ноль. Основание a может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому что a0 = 1 — это прямое следствие из определения.
Вот и все свойства. Обязательно потренируйтесь применять их на практике! Скачайте шпаргалку в начале урока, распечатайте ее — и решайте задачи.
Смотрите также:
- Тест к уроку «Что такое логарифм» (тяжелый)
- Как решать простейшие логарифмические уравнения
- Пробный ЕГЭ 2012. Вариант 10 (без логарифмов)
- Пробный ЕГЭ-2011 по математике, вариант №6
- Показательные функции в задаче B15
- Процент: налоги и зарплата. Считаем с помощью коэффициентов
Источник
Здравствуйте, уважаемые читатели! Практически все из нас изучали логарифмы. Кто-то в школе, в 10-11 классе, кто-то в училище или техникуме. И, наверняка, не все уже и помнят, что такое логарифм и с чем его едят 🙂 А между тем, это очень интересная и обширная тема. Многие в процессе изучения логарифмов, и не только их, задавались вопросом: зачем нам всё это? Оно и в жизни-то, возможно, нам никогда не пригодится! Можно ещё принять, что арифметика и разные там задачки на скорость/время/расстояние или цена/количество/стоимость, в жизни помогут. Но зачем все эти тригонометрии, интегралы, пределы и логарифмы!? Сегодня постараюсь Вам не только напомнить, что такое логарифмы, но и показать, что, порой, без них не обойтись. Но начнём, конечно, с определения. Вспомним, что такое логарифм.
Логарифм
Итак, логарифм – это показатель степени, в которую нужно возвести основание, чтобы получить число, стоящее под знаком логарифма. Или так: логарифм число a по основанию b – это показатель степени, в которую нужно возвести основание b, чтобы получить число a.
Определение логарифма с примером
В элементарной математике изучают логарифмы применительно к вещественным числам. Но также существуют и комплексные логарифмы. Что такое вещественные и комплексные числа можете почитать здесь.
Определение логарифмов и таблицу их значений впервые опубликовал в 1614 году шотландский математик Джон Непер. Логарифмические таблицы, расширенные и уточнённые другими математиками, повсеместно использовались для научных и инженерных расчётов более трёх веков, пока не появились электронные калькуляторы и компьютеры. Те, кто жил, учился и работал во времена СССР, ещё, наверняка помнят такую замечательную вещь, как логарифмическая линейка. Сейчас она, к моему сожалению, уже практически полностью вышла из употребления. У меня в школе была вот такая:
Логарифмическая линейка (изображения взято из открытых источников)
Для логарифмов, как и других функций, конечно же, существует множество различных формул и тождеств. Но я их здесь приводить не буду. Их без труда можно найти в любом математическом справочнике или на просторах Сети. Лучше я, как и обещал выше, приведу некоторые примеры, в которых без логарифмов просто не обойтись.
Да, безусловно, в нашей повседневной жизни логарифмы нам не понадобятся. Они не помогут, скажем, в шопинге или вождении машины, поиске информации или оплате коммунальных услуг. Но сейчас я приведу примеры, где на самом деле без логарифмов никуда. Конечно, все они являются примером сложных математических расчётов. Но это неоспоримые факты.
1. Навигация. Вот где логарифмы нашли широчайшее применение при расчётах, прокладке курсов, учитывая многие параметры: большие расстояния, кривизна земной поверхности, направление и скорость течений и ветров. Спросите любого штурмана, как всё это просчитать, и он вам ответит: как, как? – С помощью логарифмов.
2. Астрономия. Здесь тоже множество сложнейших расчётов, которые требуют учитывать одновременно разные понятия: колоссальные расстояния между различными объектами, их взаимное положение относительно друг друга и других объектов, светимость и массы звёзд, огромное количество всяческих коэффициентов для различных классов планет или звёзд, и т. д. От всего этого просто голова кругом идёт. Любой астроном или астрофизик подтвердит вам, что логарифмы незаменимы!
3. Психология. Вы будете смеяться, но это так. Существует доказанная теория психофизики, разработанная Фехнером, который говорит, что мера ощущения пропорциональна логарифму величины раздражения. Употребление логарифмических шкал продиктовано особенностями наших органов чувств: зрения, слуха и т. д. Человеческий мозг воспринимает раздражения от органов чувств не пропорционально силе раздражителя, а лишь пропорционально её логарифму. Именно поэтому ухо одинаково способно слышать шорох листьев и не оглохнуть от громкого удара станка на заводе. А глаз может заметить, как блестит снег на свету и не ослепнуть, если посмотрит на Солнце, которое в миллиарды раз ярче.
Я могу привести ещё огромное количество примеров, которые Вам покажут, что наша жизнь тесно связана с понятием логарифма. Зачастую, мы об этом даже не догадываемся, но это не умаляет тот факт, что без логарифмов никуда.
Надеюсь, Вам понравилась статья и Вы вспомнили или узнали, что такое логарифм и где он имеет непосредственное применение.
В следующей статье речь пойдёт о знаменитом числе e, которое приблизительно равно 2,718.
Спасибо, что читаете мой канал, ставите лайки и подписываетесь! Для меня это огромная мотивация для написания новых интересных статей.
P.S. В прошлой статье о факториалах я задал интересную задачку. Сколько времени в 10! секунд? Вот ответ: 6 недель или 1,5 месяца, если считать, что месяц – это 4 недели. Если Вас интересует само решение – пишите вопросы в комментариях, и я объясню.
Предыдущая статья
Следующая статья
Источник
Определение логарифма
Логарифм — это математическая функция, основанная на свойствах возведения в степень.
Значение логарифма соответствует показателю степени данной базы, равному положительному числу “b” в базе “a”, что также должна быть положительной и отличаться от 1.
Чтобы лучше понять концепцию логарифма, необходимо посмотреть на формулу логарифмического уравнения:
“a” = основание, которое должно быть больше нуля (a > 0) и отличаться от единицы (a ≠ 1).
“b” = логарифмируемое число, где b должно быть больше нуля (b > 0).
“x” = логарифм.
В этом уравнении мы хотим найти, в какую степень (х) нужно возвести a, чтобы получилось b, т. е. aˣ = b.
Например :
, потому что
Формулы и свойства логарифмов
Некоторые из основных правил логарифма:
- Когда логарифмируемое число равно основанию логарифма, логарифм всегда будет равен 1 ;
- Логарифм с любым основанием, число которого равно 1, всегда будет иметь результат равным 0 ;
- Два логарифма с одинаковым основанием всегда будут иметь одинаковые числа ;
- Если основание “а” возведено в степень логарифма с основанием “а” числа “b”, то он равен “b” ;
- В случае умножения чисел мы можем превратить их в сумму двух логарифмов с одинаковыми основаниями ;
- А в случае деления чисел мы превращаем их в вычитание двух логарифмов с одинаковыми основаниями ;
- Правило возведения в степень: логарифм в степени упрощается путём умножения степени на логарифм, сохраняя её основание и число (тоже самое делается с логарифмом в квадрате)
Формулы перехода к новому основанию:
Решение логарифмов — примеры
Пример 1
Пример 2
ОДЗ логарифма
Как определить Область Допустимых Значений логарифма:
Для определения ОДЗ логарифма мы обращаем внимание только на то, что стоит в скобках, и указываем, что вся эта часть больше ноля.
График логарифмической функции
Примерно таким образом может выглядеть график логарифмической функции (одна из линий на рисунке):
Свойства логарифмической функции :
- E (y) = R, множество значений — все действительные числа;
- область определения — множество всех положительных чисел D(y): (0;+∞);
- её график всегда проходит через точку (1;0);
- она не считается ни чётной, ни нечётной;
- у неё нет ни наибольшего, ни наименьшего значений;
- она не ограничена ни сверху, ни снизу;
- если 0<а<1 => функция убывает, а если a>1 => функция возрастает.
Логарифм Непера или натуральный логарифм
Состоит из логарифма, основанного на иррациональном числе, которое называется “число Эйлера”, пишется как “e” и приблизительно равно 2,718281. Является обратной функцией к экспоненциальной функции.
Название логарифма (“логарифм Непера”) произошло от имени его изобретателя — математика Джона Непера.
Десятичный логарифм
Это наиболее распространённая модель математических вычислений, особенно в так называемых логарифмических шкалах (или логарифмическом масштабе). Например: шкала pH, шкала Рихтера интенсивности землетрясений, шкала частоты звука — нотная шкала, и другие. И характеризуется тем, что основание (её логарифма) равно 10.
Десятичный логарифм может быть представлен без указания его основания.
История логарифма
Первоначально концепция логарифма была создана шотландским математиком Джоном Непером (1550–1617) в 17-м веке, с целью упрощения сложных тригонометрических расчётов.
Английский математик Генри Бриггс (1561–1630) также внёс свой вклад в исследования логарифма и считается одним из ответственных за улучшение десятичного логарифма и за создание его современной версии.
Этимологически слово “логарифм” образовано объединением двух греческих терминов: λόγος — “основание” и ἀριθμός — “число”.
Смотрите также значение Корреляции.
Источник