Предел и его свойства и противопоказания

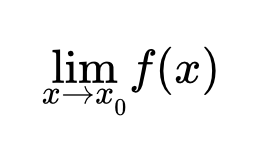
Определение предела функции

Первое определение предела функции по Гейне

Предел функции (по Гейне) при ее аргументе x, стремящемся к x0 – это такое конечное число или бесконечно удаленная точка a, для которой выполняются следующие условия:
1) существует такая проколотая окрестность точки x0, на которой функция f(x) определена;
2) для любой последовательности , сходящейся к :
,
элементы которой принадлежат окрестности , последовательность сходится к a:
.
Предел функции обозначают так:
.
Или при .
Здесь a и x0 могут быть как конечными числами, так и бесконечно удаленными точками: .
Для бесконечно удаленных точек приняты следующие обозначения:
.
Проколотая окрестность конечной точки может быть как двусторонней, так и односторонней. В последнем случае, для левой окрестности пишут:
.
Для правой окрестности:
.

С помощью логических символов существования и всеобщности это определение можно записать следующим образом:

.
См. «Универсальное определение предела функции по Гейне и по Коши».

Второе определение по Коши

Предел функции (по Коши) при ее аргументе x, стремящемся к x0 – это такое конечное число или бесконечно удаленная точка a, для которой выполняются следующие условия:
1) существует такая проколотая окрестность точки x0, на которой функция f(x) определена;
2) для любой окрестности точки a, принадлежащей , существует такая проколотая окрестность точки x0, на которой значения функции принадлежат выбранной окрестности точки a:
при .

Здесь a и x0 также могут быть как конечными числами, так и бесконечно удаленными точками. С помощью логических символов существования и всеобщности это определение можно записать следующим образом:
.

Если в качестве множества взять левую или правую окрестность конечной точки, то получим определение предела по Коши слева или справа.

Теорема
Определения предела функции по Коши и по Гейне эквивалентны.
Доказательство

Применяемые окрестности точек

В приведенном выше определении применяются произвольные окрестности точек. Например, проколотой окрестностью конечной точки является множество , где – два положительных числа, которые определяют размер окрестности. Более подробно, см. «Окрестность точки».

Тогда, фактически, определение по Коши означает следующее.
Для любых положительных чисел , существуют числа , так что для всех x, принадлежащих проколотой окрестности точки : , значения функции принадлежат окрестности точки a: ,
где , .

С таким определением не совсем удобно работать, поскольку окрестности определяются с помощью четырех чисел . Но его можно упростить, если ввести окрестности с равноудаленными концами. То есть можно положить , . Тогда мы получим определение, которое проще использовать при доказательстве теорем. При этом оно является эквивалентным определению, в котором используются произвольные окрестности. Доказательство этого факта приводится в разделе «Эквивалентность определений предела функции по Коши».

Тогда можно дать единое определение предела функции в конечных и бесконечно удаленных точках:
.
Здесь для конечных точек
; ;
.
Любые окрестности бесконечно удаленных точек являются проколотыми:
; ; .

См. «Окрестность точки»

Далее мы приводим формулировки определений предела функции по Коши для разных случаев, используя определения окрестностей с равноудаленными концами.

Конечные пределы функции в конечных точках

Число a называется пределом функции f(x) в точке x0, если
1) функция определена на некоторой проколотой окрестности конечной точки ;
2) для любого существует такое , зависящее от , что для всех x, для которых , выполняется неравенство
.

С помощью логических символов существования и всеобщности определение предела функции можно записать следующим образом:
.

Односторонние пределы.
Левый предел в точке (левосторонний предел):
.
Правый предел в точке (правосторонний предел):
.
Пределы слева и справа часто обозначают так:
; .

См. «Определение предела функции в конечной точке»

Конечные пределы функции в бесконечно удаленных точках

Аналогичным образом определяются пределы в бесконечно удаленных точках.
.
.
.

См. «Определение предела функции на бесконечности»

Бесконечные пределы функции

Также можно ввести определения бесконечных пределов определенных знаков, равных и :
.
.

Свойства и теоремы предела функции

Далее мы считаем, что рассматриваемые функции определены в соответствующей проколотой окрестности точки , которая является конечным числом или одним из символов: . Также может быть точкой одностороннего предела, то есть иметь вид или . Окрестность является двусторонней для двустороннего предела и односторонней для одностороннего.

Основные свойства

Если значения функции f(x) изменить (или сделать неопределенными) в конечном числе точек x1, x2, x3, … xn, то это изменение никак не повлияет на существование и величину предела функции в произвольной точке x0.

Если существует конечный предел , то существует такая проколотая окрестность точки x0, на которой функция f(x) ограничена:
.

Пусть функция имеет в точке x0 конечный предел, отличный от нуля:
.
Тогда, для любого числа c из интервала , существует такая проколотая окрестность точки x0, что для ,
, если ;
, если .

Если, на некоторой проколотой окрестности точки , – постоянная, то .

Если существуют конечные пределы и и на некоторой проколотой окрестности точки x0
,
то .

Если , и на некоторой окрестности точки
,
то .
В частности, если на некоторой окрестности точки
,
то если , то и ;
если , то и .

Если на некоторой проколотой окрестности точки x0:
,
и существуют конечные (или бесконечные определенного знака) равные пределы:
, то
.

Доказательства основных свойств приведены на странице
«Основные свойства предела функции».

Арифметические свойства предела функции

Пусть функции и определены в некоторой проколотой окрестности точки . И пусть существуют конечные пределы:
и .
И пусть C – постоянная, то есть заданное число. Тогда
;
;
;
, если .

Если , то .

Доказательства арифметических свойств приведены на странице
«Арифметические свойства предела функции».

Критерий Коши существования предела функции

Теорема
Для того, чтобы функция , определенная на некоторой проколотой окрестности конечной или бесконечно удаленной точки x0, имела в этой точке конечный предел, необходимо и достаточно, чтобы для любого ε > 0 существовала такая проколотая окрестность точки x0, что для любых точек и из этой окрестности, выполнялось неравенство:
.

«Доказательство критерия Коши».

Предел сложной функции

Теорема о пределе сложной функции
Пусть функции и имеют пределы:
;
.
И пусть существует такая проколотая окрестность точки , на которой
.
Тогда существует предел сложной функции , и он равен :
.
Здесь – конечные или бесконечно удаленные точки: . Окрестности и соответствующие им пределы могут быть как двусторонние, так и односторонние.
Доказательство

Теорема о пределе сложной функции применяется в том случае, когда функция не определена в точке или имеет значение, отличное от предельного . Для применения этой теоремы, должна существовать проколотая окрестность точки , на которой множество значений функции не содержит точку :
.

Если функция непрерывна в точке , то знак предела можно применять к аргументу непрерывной функции:
.
Далее приводится теорема, соответствующая этому случаю.

Теорема о пределе непрерывной функции от функции
Пусть существует предел функции t = g(x) при x → x0, и он равен t0:
.
Здесь точка x0 может быть конечной или бесконечно удаленной: .
И пусть функция f(t) непрерывна в точке t0.
Тогда существует предел сложной функции f(g(x)), и он равен f(t0):
.

Доказательство теоремы приводится на странице
«Предел и непрерывность сложной функции».

Бесконечно малые и бесконечно большие функции

Бесконечно малые функции

Бесконечно малая функция при – это такая функция , предел которой при равен нулю:
.

Сумма, разность и произведение конечного числа бесконечно малых функций при является бесконечно малой функцией при .

Произведение функции, ограниченной на некоторой проколотой окрестности точки , на бесконечно малую при является бесконечно малой функцией при .

Для того, чтобы функция имела конечный предел , необходимо и достаточно, чтобы
,
где – бесконечно малая функция при .

Доказательства свойств изложены в разделе
«Свойства бесконечно малых функций».

Бесконечно большие функции

Бесконечно большая функция при – это такая функция , предел которой при равен бесконечности:
.

Свойства бесконечно больших функций

Сумма или разность ограниченной функции, на некоторой проколотой окрестности точки , и бесконечно большой функции при является бесконечно большой функцией при .

Если функция является бесконечно большой при , а функция – ограничена, на некоторой проколотой окрестности точки , то
.

Если функция , на некоторой проколотой окрестности точки , удовлетворяет неравенству:
,
а функция является бесконечно малой при :
, и (на некоторой проколотой окрестности точки ), то
.

Cм. также: Свойства неравенств с бесконечно большими функциями ⇑.

Доказательства свойств изложены в разделе
«Свойства бесконечно больших функций».

Связь между бесконечно большими и бесконечно малыми функциями

Из двух предыдущих свойств вытекает связь между бесконечно большими и бесконечно малыми функциями.

Если функция являются бесконечно большой при , то функция является бесконечно малой при .

Если функция являются бесконечно малой при , и , то функция является бесконечно большой при .

Связь между бесконечно малой и бесконечно большой функцией можно выразить символическим образом:
, .

Если бесконечно малая функция имеет определенный знак при , то есть положительна (или отрицательна) на некоторой проколотой окрестности точки , то этот факт можно выразить так:
.
Точно также если бесконечно большая функция имеет определенный знак при , то пишут:
.

Тогда символическую связь между бесконечно малыми и бесконечно большими функциями можно дополнить следующими соотношениями:
, ,
, .

Дополнительные формулы, связывающие символы бесконечности, можно найти на странице
«Бесконечно удаленные точки и их свойства».

Пределы монотонных функций

Строго возрастающая функция Функция , определенная на некотором множестве действительных чисел X называется строго возрастающей, если для всех таких что выполняется неравенство:
. Строго убывающая функция Функция называется строго убывающей, если для всех таких что выполняется неравенство:
. Неубывающая функция Функция называется неубывающей, если для всех ; :
. Невозрастающая функция Функция называется невозрастающей, если для всех ; :
. Монотонная функция Функция называется монотонной, если она неубывающая или невозрастающая.

Отсюда следует, что строго возрастающая функция также является неубывающей. Строго убывающая функция также является невозрастающей.

Теорема
Пусть функция не убывает на интервале , где .
Если она ограничена сверху числом M: , то существует конечный предел . Если не ограничена сверху, то .
Если ограничена снизу числом m: , то существует конечный предел . Если не ограничена снизу, то .

Если точки a и b являются бесконечно удаленными, то в выражениях под знаками пределов подразумевается, что .
Эту теорему можно сформулировать более компактно.

Пусть функция не убывает на интервале , где . Тогда существуют односторонние пределы в точках a и b:
;
.

Аналогичная теорема для невозрастающей функции.

Пусть функция не возрастает на интервале , где . Тогда существуют односторонние пределы:
;
.

Доказательство теоремы изложено на странице
«Пределы монотонных функций».

Определение функции, верхней и нижней грани

Функцией y = f(x) называется закон (правило), согласно которому, каждому элементу x множества X ставится в соответствие один и только один элемент y множества Y.

Элемент x ∈ X называют аргументом функции или независимой переменной.
Элемент y ∈ Y называют значением функции или зависимой переменной.

Множество X называется областью определения функции.
Множество элементов y ∈ Y, которые имеют прообразы в множестве X, называется областью или множеством значений функции.

Более подробно, см. страницы: «Определение функции»; «Способы задания функций».

Если это особо не оговорено, мы рассматриваем функции, области определения и множества значений которых принадлежат множеству действительных чисел.

Ограниченная функция Действительная функция называется ограниченной сверху (снизу), если существует такое число M, что для всех выполняется неравенство:
.
Числовая функция называется ограниченной, если существует такое число M, что для всех :
. Верхняя грань функции Верхней гранью или точной верхней границей действительной функции называют наименьшее из чисел, ограничивающее область ее значений сверху. То есть это такое число s, для которого для всех и для любого , найдется такой аргумент , значение функции от которого превосходит s′: .
Верхняя грань функции может обозначаться так:
. Нижняя грань функции Нижней гранью или точной нижней границей действительной функции называют наибольшее из чисел, ограничивающее область ее значений снизу. То есть это такое число i, для которого для всех и для любого , найдется такой аргумент , значение функции от которого меньше чем i′: .
Нижняя грань функции может обозначаться так:
.

Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов. Опубликовано: 04-04-2018 Изменено: 09-06-2020

Источник

Предел функции и его свойства

Определение Коши используется для обоснования существования предела, а опред-ие Гейна – для обоснования отсутствия предела.

Свойства предела : предел единственен и фун-ия в некоторой окрестности предельной точки ограничена.

Определение пределов по Гейне. Число А назывется пределом функции f(x) в т x0, если для для любой сходящейся к x0 последовательности (1) значений x, отличных от x0 соответствует последовательность (2), сходящаяся к числу А.

lim x→x0 f(x) = A

(1) f(x)=c; любое x0

x1, x2, x3…→x0

c, c, c,c…→c limx→x0c=c

(2) f(x)=x; любое x0

x1; x2; x3…→x0

x1; x2; x3…→x0 limx→x0x=x0

Определение пределов по Коши. Число А называется пределом функции f(x) в т x0, если для любого ε>0 δ=δ(ε), что ля всех x, удовлетворяющих условию или приним. δ – окрестности х0 |x-x0|<δ x≠x0

|f(x)-A|<ε

-δ<x-x0<δ

-δ+x0<x<δ+x0

1) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

2)Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

3) Предел произведения функции на постоянную величину

Постоянный коэффициент можно выносить за знак предела:

4)Предел произведения

Предел произведения двух функций равен произведению пределов этих функций:

5)Предел частногоПредел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

если

Односторонние пределы. Существование предела в точке

Число А называется правым(левым) пределом функции f(x), если для любого ε>0 существует δ=δ(ε), что для всех x, отвеч неравенству x0<x<x0+δ (x0-δ<x<x0) => |f(x)- A|<ε

f(x) всегда имеет предел в т х0 тогда и только тогда, когда в этой точке существует как правый так и левый пределы, при этом они равны.

Сущ-ие предела в точке. Число А назыв. пределом фун-ии f(x) при х, стремящемся к х0 (или точке х0), если для любого, даже сколь угодно малого положительного числа ε>0, найдётся такое положительное число δ>0 (зависящее от ε, δ=δ(ε)), что для всех х, не равных х0 и удовлетворяющее условию , выполняется неравенство

Обозначается или

Теоремы о пределах функций

*пусть f(x) g(x) имеют в точке х0 пределы, соотв В и С

lim x→x0f(x)=B lim x→x0g(x)=C

f(x)±g(x)=B+C

f(x)*g(x)=B*C

f(x)/g(x) (если g(x)≠0)=B/C

Следствие

Постоянный множитель можно выносить за знак предела

*пусть функции f(x) g(x) k(x) оперделены в некоторой окрестности т х0 за искл самой х0 *пусть функции f(x) и k(x) имеет в точке х0 предел А и пусть имеет место неравенство f(x)≤g(x)≤k(x), тогда limg(x)x→x0=A

*будем говорить, что f(x)/g(x) есть неопределенность вида 0/0 или бесконечность/бесконечность если числитель и знаменатель одновременно стремятся к 0 или бесконечности limx→бесконечностиPn(x)/Qm(x)=

1)если m=n отношение коэф при х в макс степени

2)Если n>m –бесконечность

3)если n<m 0

* фун-ия не может иметь более одного предела

Сравнение бесконечно больших и бесконечно малых функций

Функция αn называется бесконечно малой функцией при x→x0, если ее предел равен 0.

Если α(x) и β(x) – бесконечно малые функции и limx→x0 β(x)/α(x)=0, то функция β(x) называется бесконечно малой функцией высшего порядка малости относительно α(x), что записывается в виде β=o(α).

Если limx→x0 β(x)/αk(x)=A (отличное от 0 конечное число), то β(x) называется бесконечно малой функцией k-го порядка малости относительно α(x).

Если limx→x0 β(x)/α(x)=1, то β(x) и α(x) называются эквивалентными бесконечно малыми функциями: β(x)~α(x).

, то это бесконечно малые фун-ии одного порядка

Первый и второй замечательные пределы

Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, называется первым замечательным пределом. Этот предел равен единице.

Предел последовательности

называется вторым замечательным пределом. Этот предел равен числу e:

Понятие производной . геометрический и физический смысл.

Производной фун-ии назыв. предел отношения приращения фун-ии к приращению независимой переменной при стремлении последнего к нулю (если этот предел сущ-ет):

Нахождении производ. фун-ии назыв. дифференцированием этой фун-ии.

Геометрич. смысл произв-ой: производная есть угловой коэффициент (тангенс угла наклона) касательной, проведённой к кривой

Физич. смысл производной: производная пути по времени есть скорость точки в момент :

Теоремы о производных

Сформулируем некоторые теоремы о производных.

Теорема. Если существуют производные и функций и , то существует

;

Следствие. так как (т.е. постоянный множитель выносится за знак производной.

Теорема. Если функция в точке имеет производную, то она в этой точке непрерывна.

Обратное неверно. На рис. 30 изображена непрерывная функция, у которой в точке нет производной.

Теорема о производной сложной функции. Пусть функция имеет производную в точке , а функция имеет производную в точке . Тогда сложная функция имеет производную в точке , причем .

Короче: в произвольной точке .

Теорема Ролля

Пусть функция y=f(x) определена и непрерывна на отрезке [a,b], дифференцируема ∀x ∈(a,b) и f(a)=f(b), тогда существует точка x=c ∈(a,b), в которой f'(c)=0.

Теорема Лагранжа

Пусть функция y=f(x) определена и непрерывна на отрезке [a,b], дифференцируема ∀x ∈(a,b), тогда существует точка x=c∈(a,b), такая, что выполняется условие f(b)-f(a)=f’(c)(b-a).

Теорема Коши

Пусть функции y=f(x) и y=g(x) непрерывны, определены на отрезке [a,b] и дифференцируемы ∀x ∈(a,b). Пусть также g'(x)≠0, тогда существует точка x=c∈(a,b), такая, что для нее выполняется условие f(b)-f(a)/g(b)-g(a)=f’(c)/g’(c).

20. Правила Лопиталя раскрытия неопределенностей:

1) Если limxàx0f(x)=limxàx0φ(x)=0, то limxàx0f(x)/φ(x)=(0/0)=limxàx0f’(x)/φ’(x) при условии, что предел в правой части выражения существует; аналогично, если limxàx0f'(x)=limxàx0φ’(x)=0, то limxàx0f’(x)/φ’(x)=(0/0)=limxàx0f’’(x)/φ’’(x) при условии, что предел в правой части существует и т.д.

2) Если limxàx0f(x)=limxàx0φ(x)=∞, то limxàx0f(x)/φ(x)=(∞/∞)=limxàx0f’(x)/φ’(x) при условии, что предел в правой части выражения существует; аналогично, если limxàx0f(x)=limxàx0φ(x)=∞, то limxàx0f(x)/φ(x)=(∞/∞)=limxàx0f’(x)/φ’(x) при условии, что предел в правой части существует, и т.д.

21. Формула тейлора ,

где – остаточный член формулы Тейлора:

Точки перегиба

Если в точке M(x0, f(x0)) графика функции y=f(x) выпуклость вверх меняется на выпуклость вниз или наоборот, то точка M(x0, f(x0)) называется точкой перегиба.

Теорема(необходимое условие точки перегиба). Если в точке M(x0, f(x0)) график функции y=f(x) имеет точку перегиба, а сама функция имеет непрерывную вторую производную, тогда f”(x) в точке x0 обращается в 0, т.е. f’’(x0)=0.

Точки графика функции, в которых вторая производная равна 0 или не существует, называются критическими точками II рода.

Теорема(достаточное условие точки перегиба). Пусть функция y=f(x) имеет вторую производную в окрестности точки x0 и пусть в самой точке f”(x0)=0 или f’’(x0) не существует. Тогда, если в указанной окрестности f”(x) имеет разные знаки слева и справа от точки x0, график функции имеет перегиб в точке M(x0, f(x0)).

Асимптоты

Прямая линия L называется асимптотой графика функции y=f(x), если расстояние от точки M(x,y), лежащей на кривой, до прямой L стремиться к нулю при неограниченном удалении этой точки от начала координат (т.е. при стремлении хотя бы одной из координат точки к бесконечности).

Существуют вертикальные, горизонтальные и наклонные асимптоты.

Если limxàaf(x)=+∞ или limxàaf(x)= – ∞, то прямая x=a является вертикальной асимптотой графика функции y=f(x).

Если limxà+∞f(x)=b или limxà-∞f(x)=b, то прямая y=b является горизонтальной асимптотой графика функции y=f(x).

Прямая y=kx+b является наклонной асимптотой графика функции y=f(x), если существуют одновременно пределы:

k=limxà+∞f(x)/x, b=limxà+∞(f(x)-kx)

или

k=limxà-∞f(x)/x, b=limxà-∞(f(x)-kx).

Производная неявной функции

Если функция y=y(x) задана неявно уравнением F(x,y)=0 , F(x,y) — дифференцируемая функция и F ‘y( x, y) не равен 0, то производная y'(x) вычисляется по формуле y'(t) = – F’x(x, y) / F’y(x, y)

(с тремя переменными еще)

Производная по направлению

Пусть z=f(x, y) определена в некоторой окрестности точки M(x, y), пусть l0=(cosα, cosβ) – единичный вектор, задающий направление прямой L, проходящей через точку M(x, y). Выберем на прямой L точку M1(x1, y1)= M(x, y)+τ*l0. Рассмотрим приращение функции ∆z=z(M1)-z(M)=f(x+ τ cosα, y+τ cosβ)-f(x, y) в точке M(x, y).

Предел отношения limτ→0 f(x+ τ cosα, y+τ cosβ)-f(x, y)/τ, если он существует, называется производной функции z=f(x, y) в точке M(x, y) по направлению l0=(cosα, cosβ) и обозначается ∂z/∂l.

Если функция z=f(x, y) имеет в точке M(x, y) непрерывные частные производные, то в этой точке существует и производная по любому направлению, исходящему из точки M(x, y); вычисляется эта производная по формуле ∂z/∂l=∂z/∂x* cosα+∂z/∂y* cosβ, где cosα и cosβ – направляющие косинусы вектора l0.

36. Градиентом функции z=f(x, y) в точке M(x, y) называется вектор с началом в точке M0, координаты которого равны соответствующим частным производным ∂z/∂x и ∂z/∂y, вычисленным в точке M(x, y).

Градиент обозначается grad z=(∂z/∂x, ∂z/∂y).

Аналогично определяются производная по направлению и градиент для функции трех переменных u=f(x,y,z) в точке M(x, y, z):

∂u/∂l=∂u/∂x*cosα+∂u/∂y*cosβ+∂u/∂z*cosγ;

grad u(M)=( ∂u/∂x, ∂u/∂y, ∂u/∂z), где cosα, cosβ, cosγ – направляющие косинусы единичного вектора l0. Градиент есть вектор, указывающий направление наибольшего возрастания функции u=f(M).

Условный экстремум

1) Усл-ый экстремум (метод множ-ей Лагранжа):

Постановка задачи: Найти экстремумы ф-ии Z=f(x,y) при усл, что φ(x,y)=0. Составляют ф-ию Лагранжа:

L=f(x,y) + η φ(x,y) ; η – множ-ль Лагранжа.

Для того, чтобы найти т экстремума, находят стац-е точки ф-ии Лагранжа, т.е. решают систему:

Достат-ое усл экстремума: Если опред-ль ∆>0, то экстр-м есть и при том max; Если ∆<0 => экст-м есть – min

вычисленный в точке (x0, y0, λ 0) (стац т).

Метод наименьших квадратов.

(x1; y1)

(x2; y2)

(xn; yn)

Подобрать теоретич. прямую вида y=ax+b “наилучшим образом” согласующуюся с этими данными.

δi=yi теор – yi эмпирич; МНК:∑(δi)2→min